István Juhász, Lajos Soukup and William Weiss
Let
![]() denote the class of all cardinal sequences of
length
denote the class of all cardinal sequences of
length ![]() associated with compact scattered spaces (or
equivalently, superatomic boolean algebras). Also put
associated with compact scattered spaces (or
equivalently, superatomic boolean algebras). Also put
We show that
![]() iff for some natural number
iff for some natural number ![]() there are infinite cardinals
there are infinite cardinals
![]() and ordinals
and ordinals
![]() such that
such that
![]() and
and
![]() where each
where each
![]() .
.
Under GCH we prove that if
![]() then
then
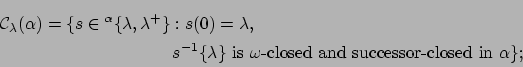
Key words and phrases:
2000 Mathematics Subject Classification:
Downloading the paper