How to split antichains in infinite posets
Péter L. Erdos and Lajos Soukup
A maximal antichain 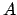 of poset
of poset 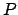 splits if and only if
there is a set
splits if and only if
there is a set
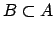 such that for each
such that for each 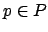 either
either 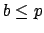 for some
for some 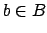 or
or 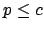 for some
for some
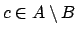 . The
poset
. The
poset 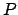 is cut-free if and only if there are no
is cut-free if and only if there are no 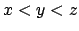 in
in 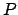 such that
such that
![$ {[x,z]_{}}_P ={[x,y]_{}}_P\cup {[y,z]_{}}_P$](img10.png) .
By [1] every maximal antichain in a finite
cut-free poset splits. Although this statement for infinite
posets fails (see [2]) we prove here that if a maximal
antichain in a cut-free poset ``resembles'' to a finite set then
it splits. We also show that a version of this theorem is just
equivalent to Axiom of Choice .
.
By [1] every maximal antichain in a finite
cut-free poset splits. Although this statement for infinite
posets fails (see [2]) we prove here that if a maximal
antichain in a cut-free poset ``resembles'' to a finite set then
it splits. We also show that a version of this theorem is just
equivalent to Axiom of Choice .
We also investigate possible strengthening of
the statements that ``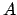 does not split'' and we could find
a maximal strengthening.
does not split'' and we could find
a maximal strengthening.
-
- 1
- R. Ahlswede - P.L. Erdos - N. Graham: A
splitting property of maximal antichains, Combinatorica 15 (1995), 475-480.
- 2
- R. Ahlswede - L. H. Khachatrian: Splitting properties in
partially ordered sets and set systems, in Numbers,
Information and Complexity (Althöfer et. al. editors) Kluvier
Academic Publisher, (2000), 29-44.
- 3
- F. Bernstein: Zur Theorie der triginomischen
Reihen, Leipz. Ber (Berichte über die Verhandlungen der
Königl. Sächsischen Gesellschaft der Wissenschaften zu
Leipzig. Math.-phys. Klasse) 60 (1908), 325-338.
- 4
- D. Duffus - B. Sands: Finite distributive lattices and the
splitting property, Algebra Universalis 49 (2003),
13-33.
- 5
- Mirna Dzamonja: Note on splitting property in
strongly dense posets of size
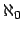 , Radovi Matematicki 8 (1992), 321-326.
, Radovi Matematicki 8 (1992), 321-326.
- 6
- P.L. Erdos: Splitting property in infinite
posets, Discrete Mathematics 163 (1997), 251-256.
- 7
- P.L. Erdos: Some generalizations of property
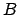 and the splitting property, Annals of Combinatorics 3
(1999), 53-59.
and the splitting property, Annals of Combinatorics 3
(1999), 53-59.
- 8
- T. Jech, Set Theory, Springer-Verlag,
Berlin Heilderberg New York 2003.
- 9
- J. Klimó, On the minimal coverint of infinite sets,
Discrete Applied Mathematics, 45 (1993) 161-168.
Key words and phrases:
2000 Mathematics Subject Classification:
Downloading the paper
![]() of poset
of poset ![]() splits if and only if
there is a set
splits if and only if
there is a set
![]() such that for each
such that for each ![]() either
either ![]() for some
for some ![]() or
or ![]() for some
for some
![]() . The
poset
. The
poset ![]() is cut-free if and only if there are no
is cut-free if and only if there are no ![]() in
in ![]() such that
such that
![]() .
By [1] every maximal antichain in a finite
cut-free poset splits. Although this statement for infinite
posets fails (see [2]) we prove here that if a maximal
antichain in a cut-free poset ``resembles'' to a finite set then
it splits. We also show that a version of this theorem is just
equivalent to Axiom of Choice .
.
By [1] every maximal antichain in a finite
cut-free poset splits. Although this statement for infinite
posets fails (see [2]) we prove here that if a maximal
antichain in a cut-free poset ``resembles'' to a finite set then
it splits. We also show that a version of this theorem is just
equivalent to Axiom of Choice .
![]() does not split'' and we could find
a maximal strengthening.
does not split'' and we could find
a maximal strengthening.