Projective 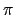 -character bounds the order of a
-character bounds the order of a 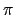 -base
-base
István Juhász,
and Zoltán Szentmiklóssy
All spaces below are Tychonov. We define the projective
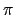 -character
-character
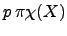 of a space
of a space 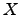 as the supremum of the
values
as the supremum of the
values
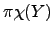 where
where 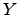 ranges over all continuous images of
ranges over all continuous images of
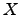 . Our main result says that every space
. Our main result says that every space 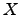 has a
has a 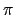 -base
whose order is
-base
whose order is
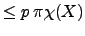 , that is every point in
, that is every point in 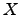 is
contained in at most
is
contained in at most
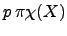 -many members of the
-many members of the 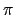 -base. Since
-base. Since
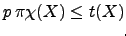 for compact
for compact 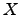 , this provides a significant
generalization of a celebrated result of Shapirovskii.
, this provides a significant
generalization of a celebrated result of Shapirovskii.
Key words and phrases:
Projective pi-character, order of a pi-base,
irreducible map
2000 Mathematics Subject Classification:
54A25, 54C10, 54D70
Downloading the paper