Resolvability of spaces having small spread or extent
István Juhász, Lajos Soukup and Zoltán Szentmiklóssy
In a recent paper O. Pavlov proved the following two interesting
resolvability results:
- If a space
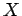 satisfies
satisfies
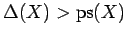 then
then
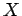 is maximally resolvable.
is maximally resolvable.
- If a
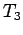 -space
-space 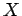 satisfies
satisfies
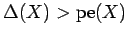 then
then
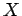 is
is 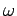 -resolvable.
-resolvable.
Here
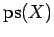 (
(
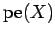 ) denotes the smallest successor
cardinal such that
) denotes the smallest successor
cardinal such that 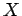 has no discrete (closed discrete) subset of
that size and
has no discrete (closed discrete) subset of
that size and 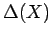 is the smallest cardinality of a non-empty
open set in
is the smallest cardinality of a non-empty
open set in 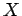 . In this note we improve (1) by showing that
. In this note we improve (1) by showing that
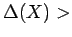
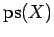 can be relaxed to
can be relaxed to
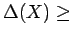
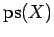 . In particular,
if
. In particular,
if 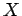 is a space of countable spread with
is a space of countable spread with
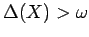 then
then
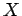 is maximally resolvable.
is maximally resolvable.
The question if an analogous improvement of (2) is valid remains
open, but we present a proof of (2) that is simpler than Pavlov's.
-
- 1
-
O. Pavlov, On resolvability of topological spaces
Topology and its Applications 126 (2002) 37-47.
2000 Mathematics Subject Classification: 54A25, 54B05
Key words and phrases: 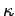 -resolvable space, maximally resolvable space,
dispersion character, spread, extent
-resolvable space, maximally resolvable space,
dispersion character, spread, extent
Downloading the paper
![]() -resolvable space, maximally resolvable space,
dispersion character, spread, extent
-resolvable space, maximally resolvable space,
dispersion character, spread, extent